In this talk, we generalize universal property of quotients (UPQ) into arbitrary categories. UPQs in algebra and topology and an introduction to categories will be given before the abstraction. As in the discovery of any universal properties, the existence of quotients in the category of sets and that of groups will be presented.

If you have not yet been exposed to group theory, please read Monoids and Groups for an introduction.

When I was doing abstract algebra, I was amazed by the similarities of the Universal Property of Quotients in various algebraic structures. Let us start with reviewing the universal property of quotients in groups, rings, $R$-modules, sets, and topological spaces.

UPQ in Grp/Ring/R-Mod/Set/Top

Let $A$ be a group/ring/R-module/set/topological space. Let $E \subseteq A$ be a normal subgroup/ideal/submodule or in the case of sets or topological spaces $E \subseteq A^2$ equivalence relation. We have the following diagram:

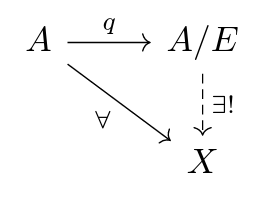
i.e. for all homomorphisms $f : A \to X$, there is a unique homomorphism $A/E \to X$ such that $\overline{f} ∘ q = f$ if and only if $E \subseteq \operatorname{ker}(f)$ or in the case of sets and topological spaces we have that $x E y \implies f(x) = f(y)$ for all $x,y ∈ A$.

Example. Note that $\mathbf{Z}$ is an additive group/ring/$\mathbf{Z}$-module and $2\mathbf{Z}$ is a normal subgroup/ideal/$\mathbf{Z}$-submodule. We have a quotient homomorphism $q : \mathbf{Z} \to \mathbf{Z}/2\mathbf{Z}$ given by $n \to n + 2\mathbf{Z}$.

Example. We have a (continuous) quotient map $[0,1] \to S^{1} ≅ [0,1]/∼$ where $x ∼ y$ if and only if $x = y$ or $\{x,y\} ⊆ \{0,1\}$.

Introduction to Categories

Here is a sketch of a definition of a category.

Definition. A category is the following data:

1. objects, denoted $\operatorname{ob}(C)$ (note this need not be a set)

2. homomorphisms for every $A,B ∈ \operatorname{ob}(\mathcal{C})$, which we denote by $f : A \to B$. We denote the collection of homomorphisms from $A$ to $B$ by $\operatorname{Hom}_{\mathcal{C}}(A,B)$.

3. An associative way to compose: for all $f : A \to B$, $g : B \to C$, $h : C \to D$, $(h ∘ g) ∘ f = h ∘ (g ∘ f)$.

satisfying axioms of a category.

Examples. Set, Grp, Ring, R-Mod, Topological spaces. All of these are examples are concrete categories.

UPQ in Categories

Intuitively, quotients are used to identify elements of an object in a concrete category to get the "closest" object that is in the same category.

Definition. Let $\mathcal{C}$ be a concrete category (there is a forgetful functor from $\mathcal{C}$ to $\mathrm{Set}$). Let $A ∈ \operatorname{ob}(\mathcal{C})$. We can talk about $P \subseteq \mathcal{P}(A)$, a set of nonempty disjoint subsets of $A$. A quotient of $A$ by $P$ in $\mathcal{C}$ is a universal object in the category of $\mathcal{D} \leq \mathcal{C}^{A}$ where

In other words, $q : A \to \overline{A}$ is a quotient if and only if

1. $q : A \to \overline{A} ∈ \operatorname{Hom}_{\mathcal{C}}(A,\overline{A})$ and for all $S ∈ P, q(a) = q(b)$ for all $a,b ∈ S \subseteq A$

2. for all $f : A \to X$ satisfying (1), there is a unique $\overline{A} \to C$ in $\mathcal{C}$ such that the diagram commutes:

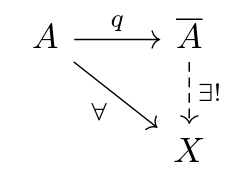
Remark. Since a quotient is a universal object which is unique up to unique isomorphism, we can say the quotient of $A$ by $P$.

Proposition. (UPQ) Let $q : A \to \overline{A}$ be the quotient of $A$ by $P$ in $\mathcal{C}$, a concrete category. Let $f : A \to X$ be in $\mathrm{Set}$. Then there exists a unique $\overline{f} : \overline{A} \to X$ such that the following diagram commutes if and only if $f$ satisfies condition (1) above.

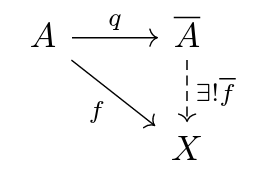
Proof. The backward direction is clear by condition (2). Let us check the forward direction. Since $\overline{f}, q$ are in $\mathcal{C}$, $f = \overline{f} ∘ q$ is in $\mathcal{C}$. Also for all $S ∈ P$ we have for all $a,b ∈ S$, $f(a) = \overline{f} ∘ q(a) = \overline{f} ∘ q(b) = f(b)$

Existence of Quotients in Set and Grp

Useful exercise. There is a one-to-one correspondence of equivalence relations on $X$ and the collection of partitions on $X$ (where $X$ is a set), given by $E \to P_{E}$, the equivalence classes of $E$.

Proposition. The quotients exist in $\mathrm{Set}$ and $\mathrm{Grp}$.

Sketch of proof. Let $A ∈ \operatorname{ob}(\mathcal{C})$. Let $P \subseteq \mathcal{P}(A)$ be disjoint.

In the category $\mathrm{Set}$ we let

which is a partition on $A$. The quotient map $q : A \to \overline{A}$ is given by $y = q(x)$ if and only if $x ∈ y$.

In $\mathrm{Grp}$ we let $\overline{A} : A/N$ where $N = ⟨\{axa^{-1} : a ∈ A, x ∈ S\}⟩$ is the normal closure of $S$, where

for $C ∈ P$, $S = \bigcup_{C ∈ P} S_C$. Let $q : A \to A/N$ be the quotient map.

Remark. If $N ⊴ A$ a normal subgroup of a group, then $q : A \to A/N$ is the quotient of $A$ by ${N}$ in $\mathrm{Grp}$.

Exercise. Check the existence in $\mathrm{Ring}$, $\mathrm{R-Mod}$ and $\mathrm{Top}$.

Non-Existence of Quotients in Field

Let us show that there is no nontrivial quotients in the category of fields.

Proposition. Nontrivial quotients do not exist in $\mathrm{Field}$. That is, for all field $A$, there is no quotient of $A$ by $P$ in $\mathrm{Field}$ where $P ≠ ∅$ and not a set of singletons in $A$.

Proof. Assume toward a contradiction that there is the quotient$q : A \to \overline{A}$. Since $A$ is a field, we have $q$ is one to one. But exists $\mathrm{C} ∈ P$ and $a ≠ b$ in $C$ such that $q(a) = q(b)$ and this is our contradiction.

Application and Further

Definition. Let $M,N$ be $R$-modules where $R$ is a commutative ring. A tensor product of $M, N$ over $R$ is an R-bilinear map $⊗: M × N → M ⊗_R N$ such that for all $R$-bilinear maps $M \times N \to L$, there exists a unique $M ⊗_R N \to L$ $R$-module homomorphism such that the following diagram commutes.

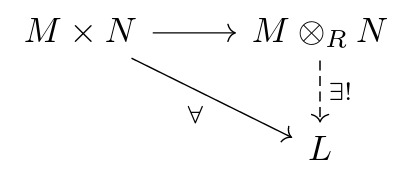
A construction of tensor products is given by the following commutative diagram:

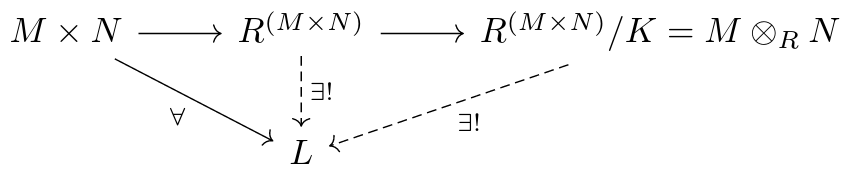
where the submodule

Fact. Let $\mathcal{C}$ be the category of an algebraic structure. Let $q : A \to \overline{A}$ the quotient of $A$ by $P$ in $\mathcal{C}$. Then $q$ is onto and $\overline{A} ≅ \{q^{-1}(a) : a ∈ A \}$ (fibers of $q$).

Note that if the quotient exists, it is always of the form $q : A \to A/\!∼$ where $∼$ is the equivalence relation induced by the fibers.

Proposition. (First Isomorphism Theorem) Let $f : A \to B$ be in a category of an algebraic structure $\mathcal{C}$. Then $A/\!∼\, ≅ \operatorname{Image}(f)$ in $\mathcal{C}$.

Note the way to relate the quotient of an object A in a concrete category to the quotient of the same $A$ in the category of Set is via the UPQ (image the diagram) in the category of Set.

This leads us naturally to a question: in a general concrete category, when is a quotient homomorphism onto? If the category has this property, then similar results as mentioned above follow.